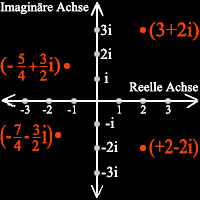-
Übersicht über den Aufbau der Zahlenbereiche - |
Natürliche
Zahlen  Ausgangspunkt
des Zahlenaufbaus sollten die natürlichen Zahlen sein. Sie werden
auch positive ganze Zahlen genannt. Mit ihnen wird man bereits in der frühen
Kindheit vertraut, anfangs noch als Teil der Sprache (vgl. Sprachentwicklung
/ Spracherwerb bzw. Sprachgeschichte)
- Zahlen sind Formen von Sprache
und Denken -, deshalb sollte auch jede zu Ende gedachte Mathematik wieder
zu einer Lingusitik werden. Die natürlichen Zahlen sind wie geschaffen für
das „Abzählen“ und bezeichnen die „Anzahlen“ von Dingen
bzw. von dem, was „ist“. Insofern sind sie also in unserer Begriffswelt
unmittelbar anwesend (zumindest dann, wenn sie „klein“ genug sind) und
bedürfen eigentlich keiner Begründung.Die
Mengenlehre begreift die natürlichen Zahlen als Äquivalenzklassen
bzw. Kardinalzahlen endlicher Mengen. Da selbst im Elementarunterricht
die Zahlen als Mengen aufgefaßt werden, verwenden wir die dort übliche
Schreibweise.Die Menge |N der natürlicheen
Zahlen wird dann wie folgt angegeben:|N = {1,
2, 3, 4, 5, ...}. Dies ist eine unendliche Menge, d.h. es gibt keine „größte
natürliche Zahl“, man kann nur zu jeder vorgegebenen beleibig viele
noch größere finden.Ganze
Zahlen  Zu
den ganzen Zahlen zählen zusätzlich die negativen Zahlen
und die Null, also nicht nur positiven ganzen Zahlen (die natürlichen
Zahlen), sondern auch die negativen ganzen Zahlen und die Null.
Wenn man nämlich fordert, daß z.B. eine Subtraktion mit natürlichen
Zahlen immer durchführbar sein soll, dann muß man neue Zahlen einführen,
die dieser Forderung gerecht werden. Diese neuen Zahlen heißen negativ,
man kennezeichnet sie mit einem Minuszeichen. Damit wird z.B. 8 - 11 = -3. Negative
Zahlen haben im täglichen Leben viele Entsprechungen. In der Buchhaltung
nennt man sie Fehlbeträge, im Bankwesen Soll oder Schulden
(bzw. Fremdkapital), in der Temperaturmessung Kältegrade oder
Minusgrade u.s.w., und als Spezialfall gibt es noch die Möglichkeit,
daß eine Zahl weder postiv noch negativ ist: Null.
Die Null kennzeichnet so das „Nichtvorhandensein“ z.B. irgendeines
Betrages. Die Mengen der natürlichen Zahlen und der negativen Zahlen zugleich
der Null vereinigt man in dem Begriff der ganzen Zahlen:|Z
= {0, +1, -1, +2, -2 +3, -3, +4, -4, +5, -5, ...}. Zum Unterschied von den negativen
Zahlen nennt man die natürlichen Zahlen jetzt positive ganze
Zahlen und kennzeichnet sie mit einem Pluszeichen. Jede positive ganze Zahl
hat ihr negatives Gegenstück, nur die Null ist ihr eigenes.Rationale
Zahlen  Die
Forderung, der Divison für beliebige Paare von ganzen Zahlen einen
Sinn zu geben, kann nur durch eine nochmalige Erweiterung des Zahlenbereichs erfüllt
werden (wenigstens bis auf eine Ausnahme). Die neu einzuführenden Zahlen
sind die Brüche, geschrieben als  (a/b; „a“ durch „b“) . Der Bruchstrich hat zwar die Funktion
des Divisonszeichens (:), aber der Bruch wird als eine Zahl aufgefaßt,
nämlich als „der b-te Teil“ von „a“. Die Zahl
über dem Bruchstrich heißt Zähler, die unter dem Bruchstrich
Nenner (gleichbedeutend mit Dividend bzw. Divisor). Man unterscheidet
echte Brüche und unechte Brüche; bei echten Brüchen
ist der Zähler kleiner als der Nenner, bei unechten Brüchen
ist der Zähler größer als der Nenner. Unechte Brüche
lassen sich stets in eine Summe aus einer ganzen Zahl und einem echten Bruch
verwandeln. Unter den echten Brüchen nehmen die Stammbrüche
eine Sonderstellung ein: sie haben die Zahl 1 zum Zähler und sind
positiv. Die Menge der Stammbrüche lautet also {1/2; 1/3; 1/4; 1/5;
...}. Die vorhin erwähnte Ausnahme besteht darin, daß eine Division
durch Null nicht definierbar ist, d.h. daß die Null als Nenner
nicht vorkommen darf. Jeder Bruch läßt sich durch Kürzen auf eine
Form bringen, bei der Zähler und Nenner keine gemeinsamen Faktoren
außer 1 besitzen. Wenn dies erreicht ist, nennt man den Bruch eine rationale
Zahl. Er repräsentiert dann eine Klasse von Brüchen mit demselben
Wert.Beispiele: 2/3 ist eine rationale Zahl,
die für {2/3; 4/6; 6/9; 8/12; ...} steht; 5/1 ist eine rationale Zahl,
die für {5/1; 10/2; 15/3; 20/4; ...} steht u.s.w.. Die Menge aller rationalen
Zahlen enthält also die der ganzen Zahlen als Teilmenge.Von
den bisher besprochenen gemeinen Brüchen zu unterscheiden sind die
Dezimalbrüche. Sie sind stets Summen von Brüchen mit Zehnerpotenzen
als Nenner.Beispiel: 0,3174 = 3/10 + 1/100
+ 7/1000 + 4/10000 = 3174/10000.|Q ist die Menge
der rationalen Zahlen. |Q ist ein „Körper“, d.h. (im Sinne
der Mengenlehre): eine Menge, in der man die vier Grundrechenarten (allgemeiner:
zwei Verknüpfungen samt ihren Umkehrungen) uneingeschränkt ausführen
darf, mit Ausnahme der Divison durch Null.
(a/b; „a“ durch „b“) . Der Bruchstrich hat zwar die Funktion
des Divisonszeichens (:), aber der Bruch wird als eine Zahl aufgefaßt,
nämlich als „der b-te Teil“ von „a“. Die Zahl
über dem Bruchstrich heißt Zähler, die unter dem Bruchstrich
Nenner (gleichbedeutend mit Dividend bzw. Divisor). Man unterscheidet
echte Brüche und unechte Brüche; bei echten Brüchen
ist der Zähler kleiner als der Nenner, bei unechten Brüchen
ist der Zähler größer als der Nenner. Unechte Brüche
lassen sich stets in eine Summe aus einer ganzen Zahl und einem echten Bruch
verwandeln. Unter den echten Brüchen nehmen die Stammbrüche
eine Sonderstellung ein: sie haben die Zahl 1 zum Zähler und sind
positiv. Die Menge der Stammbrüche lautet also {1/2; 1/3; 1/4; 1/5;
...}. Die vorhin erwähnte Ausnahme besteht darin, daß eine Division
durch Null nicht definierbar ist, d.h. daß die Null als Nenner
nicht vorkommen darf. Jeder Bruch läßt sich durch Kürzen auf eine
Form bringen, bei der Zähler und Nenner keine gemeinsamen Faktoren
außer 1 besitzen. Wenn dies erreicht ist, nennt man den Bruch eine rationale
Zahl. Er repräsentiert dann eine Klasse von Brüchen mit demselben
Wert.Beispiele: 2/3 ist eine rationale Zahl,
die für {2/3; 4/6; 6/9; 8/12; ...} steht; 5/1 ist eine rationale Zahl,
die für {5/1; 10/2; 15/3; 20/4; ...} steht u.s.w.. Die Menge aller rationalen
Zahlen enthält also die der ganzen Zahlen als Teilmenge.Von
den bisher besprochenen gemeinen Brüchen zu unterscheiden sind die
Dezimalbrüche. Sie sind stets Summen von Brüchen mit Zehnerpotenzen
als Nenner.Beispiel: 0,3174 = 3/10 + 1/100
+ 7/1000 + 4/10000 = 3174/10000.|Q ist die Menge
der rationalen Zahlen. |Q ist ein „Körper“, d.h. (im Sinne
der Mengenlehre): eine Menge, in der man die vier Grundrechenarten (allgemeiner:
zwei Verknüpfungen samt ihren Umkehrungen) uneingeschränkt ausführen
darf, mit Ausnahme der Divison durch Null.Irrationale
Zahlen  Der
Ausdruck  liefert eine irrationale Zahl, weil er - z.B. über das Beweisverfahren
- keine rationale Zahl liefert. Soll man also das Potenzieren bzw. Radizieren
mit beliebigen rationalen Zahlen (im Exponenten) durchführen können,
ist es notwendig, neue Zahlen einzuführen. Sie heißen (eben: weil sie
nicht rational sind): irrationale Zahlen. Zur Darstellung irrationaler
Zahlen eignen sich Dezimalbrüche besser als gemeine Brüche.
Jede irrationale Zahl ist ein unendlicher Dezimalbruch, hat aber im Gegensatz
zu rationalen Zahlen keine Periode. Durch „Probieren“ kann man
beliebig viele Stellen einer Wurzel finden, beispielsweise:
liefert eine irrationale Zahl, weil er - z.B. über das Beweisverfahren
- keine rationale Zahl liefert. Soll man also das Potenzieren bzw. Radizieren
mit beliebigen rationalen Zahlen (im Exponenten) durchführen können,
ist es notwendig, neue Zahlen einzuführen. Sie heißen (eben: weil sie
nicht rational sind): irrationale Zahlen. Zur Darstellung irrationaler
Zahlen eignen sich Dezimalbrüche besser als gemeine Brüche.
Jede irrationale Zahl ist ein unendlicher Dezimalbruch, hat aber im Gegensatz
zu rationalen Zahlen keine Periode. Durch „Probieren“ kann man
beliebig viele Stellen einer Wurzel finden, beispielsweise:  = 1,41421356....
Selbstverständlich gibt es zweckmäßigere Verfahren als das „Probieren“
(z.B. die Intervallschachtelung oder die Reihenentwicklung), aber sie ändern
nichts am Ergebnis. Es läßt sich zeigen, daß alle nicht aufgehenden
Wurzelausdrücke, Summen oder Produkte von Wurzeln und ganzen oder rationalen
Zahlen irrational sind. Außerdem weiß man, daß man beliebige
derartige Ausdrücke als Lösungen von „algebraischen“ Gleichungen
mit ganzzahligen Koeffizienten betrachten kann. Irrationalzahlen dieser Art
heißen daher algebraisch irrational. Nun gibt es aber noch andere
nichtperiodisch unendliche Dezimalbrüche, die nicht zu dieser Art gehören.
Beispielsweise stellt sich heraus, daß sämtliche nicht ganzzahligen
Logarithmen zwar irrational, aber nicht algebraisch irrational sind.
Auch die Kreiszahl p (p
= 3,14159265...) und die Eulersche Zahl e (e = 2,71828182...) sind solche Irrationalzahlen;
man nennt sie transzendent irrational. = 1,41421356....
Selbstverständlich gibt es zweckmäßigere Verfahren als das „Probieren“
(z.B. die Intervallschachtelung oder die Reihenentwicklung), aber sie ändern
nichts am Ergebnis. Es läßt sich zeigen, daß alle nicht aufgehenden
Wurzelausdrücke, Summen oder Produkte von Wurzeln und ganzen oder rationalen
Zahlen irrational sind. Außerdem weiß man, daß man beliebige
derartige Ausdrücke als Lösungen von „algebraischen“ Gleichungen
mit ganzzahligen Koeffizienten betrachten kann. Irrationalzahlen dieser Art
heißen daher algebraisch irrational. Nun gibt es aber noch andere
nichtperiodisch unendliche Dezimalbrüche, die nicht zu dieser Art gehören.
Beispielsweise stellt sich heraus, daß sämtliche nicht ganzzahligen
Logarithmen zwar irrational, aber nicht algebraisch irrational sind.
Auch die Kreiszahl p (p
= 3,14159265...) und die Eulersche Zahl e (e = 2,71828182...) sind solche Irrationalzahlen;
man nennt sie transzendent irrational.Reelle
Zahlen  Die
Menge |R der reellen Zahlen ergibt sich aus der Gesamtheit aller Irrationalzahlen
vereinigt mit den Rationalzahlen. |R ist wie |Q ein „Körper“.
In den Bezeichnungen der Mengenelehre gilt: |N  |Z
|Z  |Q
|Q  |R (das liest sich so: |N ist Teilmenge von |Z, |Z ist Teilmenge von |Q, |Q ist
Teilmenge von |R). Die rellen Zahlen haben eine gemeinsame Eigenschaft,
die noch nicht erwähnt wurde: wenn zwei beliebige relle Zahlen a
und b gegeben sind, läßt sich immer feststellen, welche von
beiden größer ist oder ob beide gleich sind; es gibt für a
und b nur diese drei Möglichkeiten:. a ist größer
als b (a > b), a ist kleiner als b (a
< b), a ist gleich b (a = b). Außerdem
gilt für a > b (bzw. a < b) und b
> c (bzw. b < c) sozusagen „erst recht“:
a > c (bzw. a < c). So selbstverständlich
diese Aussage scheinen mag, sie hat eine wichtige Konsequenz: jede vorgegebene
Anzahl von reellen Zahlen läßt sich „anordnen“, d.h.
hier der Größe nach ordnen.
|R (das liest sich so: |N ist Teilmenge von |Z, |Z ist Teilmenge von |Q, |Q ist
Teilmenge von |R). Die rellen Zahlen haben eine gemeinsame Eigenschaft,
die noch nicht erwähnt wurde: wenn zwei beliebige relle Zahlen a
und b gegeben sind, läßt sich immer feststellen, welche von
beiden größer ist oder ob beide gleich sind; es gibt für a
und b nur diese drei Möglichkeiten:. a ist größer
als b (a > b), a ist kleiner als b (a
< b), a ist gleich b (a = b). Außerdem
gilt für a > b (bzw. a < b) und b
> c (bzw. b < c) sozusagen „erst recht“:
a > c (bzw. a < c). So selbstverständlich
diese Aussage scheinen mag, sie hat eine wichtige Konsequenz: jede vorgegebene
Anzahl von reellen Zahlen läßt sich „anordnen“, d.h.
hier der Größe nach ordnen.Imaginäre
Zahlen  Trotz
der Einführung der Irrationalzahlen sind zum Potenzieren immer noch
nicht alle Zahlen zugelassen. Beispielsweise entspricht die Potenz  weder einer rationalen noch einer irrationalen Zahl. Es gibt eben überhaupt
keine reelle Zahl, deren Quadrat gleich -1 ist. Das liegt einfach
daran, daß das Quadrat jeder reellen Zahl (ob positiv oder
negativ) immer positiv ist. Jede andere Definition würde Widersprüche
hervorrufen. Wenn man daher den Zahlenbereich so erweitern möchte, daß
er die geraden Wurzeln aus negativen reellen Zahlen ebenfalls enthält,
dann muß man gleichzeitig die Multiplikationsvorschrift ändern. Dies
muß aber so geschehen, daß die bisherigen „normalen“ Multiplikationen
(und alle anderen Rechenarten) unveränderte Ergebnisse zeigen. Eine besondere
Rolle spielt bei der Einführung dieser neuen Zahl die Wurzel aus (-1). Es
stellt sich nämlich heraus, daß es bereits gelingt, für
weder einer rationalen noch einer irrationalen Zahl. Es gibt eben überhaupt
keine reelle Zahl, deren Quadrat gleich -1 ist. Das liegt einfach
daran, daß das Quadrat jeder reellen Zahl (ob positiv oder
negativ) immer positiv ist. Jede andere Definition würde Widersprüche
hervorrufen. Wenn man daher den Zahlenbereich so erweitern möchte, daß
er die geraden Wurzeln aus negativen reellen Zahlen ebenfalls enthält,
dann muß man gleichzeitig die Multiplikationsvorschrift ändern. Dies
muß aber so geschehen, daß die bisherigen „normalen“ Multiplikationen
(und alle anderen Rechenarten) unveränderte Ergebnisse zeigen. Eine besondere
Rolle spielt bei der Einführung dieser neuen Zahl die Wurzel aus (-1). Es
stellt sich nämlich heraus, daß es bereits gelingt, für  eine widerspruchsfreie Definition zu finden, denn zusammen mit den bisher gültigen
Rechengesetzen (-a = (-1) · a) sind dann auch alle anderen
Wurzeln
eine widerspruchsfreie Definition zu finden, denn zusammen mit den bisher gültigen
Rechengesetzen (-a = (-1) · a) sind dann auch alle anderen
Wurzeln  erklärt. Der einfachste Versuch besteht darin, für
erklärt. Der einfachste Versuch besteht darin, für  einfach ein neues Symbol zu setzen. Man nahm
einfach ein neues Symbol zu setzen. Man nahm  = i (von imaginär, weil man sich nichts darunter vorstellen
konnte), und tatsächlich kann man mit imaginären Größen
genauso rechnen wie mit reellen, ohne in Widerspruch zu geraten. Die einzige
Änderung gegenüber normalen Rechenarten ist die „erweiterte Multiplikationsregel“:i · i = i² = -1.Die
Menge aller imaginären Zahlen wird einfach dadurch erzeugt, daß
man die rellen Zahlen mit i, der imaginären Einheit, multipliziert,
z.B. 2i; 24i; -8i; 162i u.s.w.. Natürlich kann
man eine Summe aus einer reellen und einer imaginären Zahl, z.B. 1
+ i, nicht ausführen, immer aber lassen sich beliebige Summen von
imaginären und reellen Zahlen durch Zusammenfassen der gleichartigen Glieder auf die Form a + i · b bringen, wobei a
und b für reelle Zahlen stehen. Ausdrücke wie a
+ ib muß man deshalb als Ganzes betrachten. Man nennt sie
komplex.
= i (von imaginär, weil man sich nichts darunter vorstellen
konnte), und tatsächlich kann man mit imaginären Größen
genauso rechnen wie mit reellen, ohne in Widerspruch zu geraten. Die einzige
Änderung gegenüber normalen Rechenarten ist die „erweiterte Multiplikationsregel“:i · i = i² = -1.Die
Menge aller imaginären Zahlen wird einfach dadurch erzeugt, daß
man die rellen Zahlen mit i, der imaginären Einheit, multipliziert,
z.B. 2i; 24i; -8i; 162i u.s.w.. Natürlich kann
man eine Summe aus einer reellen und einer imaginären Zahl, z.B. 1
+ i, nicht ausführen, immer aber lassen sich beliebige Summen von
imaginären und reellen Zahlen durch Zusammenfassen der gleichartigen Glieder auf die Form a + i · b bringen, wobei a
und b für reelle Zahlen stehen. Ausdrücke wie a
+ ib muß man deshalb als Ganzes betrachten. Man nennt sie
komplex.Komplexe
Zahlen  Jede
komplexe Zahl „besteht“ aus zwei Komponenten: in a + b
heißt a der Realteil, b der Imaginärteil. Die Menge |K
der komplexen Zahlen ist wie |R und |Q ein „Körper“. Beispiele:
3 + 2i; 8 - 3i; -4 + 5i; -1 -3i. Der Ausdruck „imaginär“ hat etwas
Unfaßbares, Unbegreifliches an sich, was für Laien wie für Mathematiker
oft Denkschwierigkeiten verursacht. Wie soll es Zahlen geben, die man sich nicht
vorstellen kann? Dabei ist es sehr einfach, ohne das ominöse „i“
auszukommen, und eine modernere, wenn auch unpraktische Definition geht diesen
Weg: Eine komplexe Zahl wird in dieser Ausdrucksweise definiert als ein
Zahlenpaar (a; b) mit einer ersten Koordinate (a) und einer zweiten
Koordinate (b). Die erste Kordiante heißt Realteil, die zweite Imaginärteil,
aber jetzt sind diese Bezeichnungen lediglich Namen, die der Tradition wegen bestehen,
aber keinen tieferen Sinn mehr haben.Geometrische
Darstellung der komplexen Zahlen
Gauß'sche Zahlenebene als geometrische
Darstellung der komplexen Zahlen
| Wenn die
Menge der Punkte einer Geraden der Menge der reellen Zahlen zugeordnet werden
kann, dann können die imaginären Zahlen nicht auch noch auf dieser Geraden
liegen. Diesen Schluß zog schon Carl Friedrich Gauß (1777-1855 );
er erdachte eine Darstellung in einer Ebene, die noch heute unverändert verwendet
wird (Gauß'sche Zahlenebene). Es handelt sich um ein rechtwinkliges
kartesisches Koordinatensystem, dessen Abzisse den reellen Zahlen und dessen
Ordinate den imaginären Zahlen zugeordnet wird. Die komplexen Zahlen überdecken dann die gesamte Ebene (siehe Abbildung). Anwendung
komplexer Zahlen Man könnte zunächst
meinen, komplexe Zahlen seien nur für die Mathematik wichtig und auch
dort nur für die „höheren Probleme“. Doch diese Meinung entspricht
überhaupt nicht der Wirklichkeit, denn selbst einfache mathematische Probleme
werden in komplexer Schreibweise nicht nur übersichtlicher, sondern oftmals
erst lösbar (z.B. das Rechnen mit Winkelfunktionen oder die Berechnung der
Kreiszahl). Darüber hinaus sind komplexe Zahlen in der gesamten Naturwissenschaft
schlechterdings unentbehrlich. Die moderne Physik ist ohne komplexe Zahlen
überhaupt nicht denkbar. Aber selbst in der technischen Welt, vor allem in
der Elektronik, kommt man ohne sie nicht aus. Jeder Schaltplan eines Fernsehers
wird komplex berechnet. Antennen und Kabel ebenfalls. Das liegt daran, daß
sich Schwingungsvorgänge aller Art besonders einfach komplex beschreiben
lassen. (Das mag sich paradox anhören, ist aber wirklich einfacher!). Dabei
entspricht der Amplitude samt ihrer Dämpfung der Imaginärteil der Frequenz
und der Phase einer Welle. Allerdings verwenden die Elektrotechniker statt des
„i“ der Mathematik das Symbol „j“, was aber unwesentlich ist. );
er erdachte eine Darstellung in einer Ebene, die noch heute unverändert verwendet
wird (Gauß'sche Zahlenebene). Es handelt sich um ein rechtwinkliges
kartesisches Koordinatensystem, dessen Abzisse den reellen Zahlen und dessen
Ordinate den imaginären Zahlen zugeordnet wird. Die komplexen Zahlen überdecken dann die gesamte Ebene (siehe Abbildung). Anwendung
komplexer Zahlen Man könnte zunächst
meinen, komplexe Zahlen seien nur für die Mathematik wichtig und auch
dort nur für die „höheren Probleme“. Doch diese Meinung entspricht
überhaupt nicht der Wirklichkeit, denn selbst einfache mathematische Probleme
werden in komplexer Schreibweise nicht nur übersichtlicher, sondern oftmals
erst lösbar (z.B. das Rechnen mit Winkelfunktionen oder die Berechnung der
Kreiszahl). Darüber hinaus sind komplexe Zahlen in der gesamten Naturwissenschaft
schlechterdings unentbehrlich. Die moderne Physik ist ohne komplexe Zahlen
überhaupt nicht denkbar. Aber selbst in der technischen Welt, vor allem in
der Elektronik, kommt man ohne sie nicht aus. Jeder Schaltplan eines Fernsehers
wird komplex berechnet. Antennen und Kabel ebenfalls. Das liegt daran, daß
sich Schwingungsvorgänge aller Art besonders einfach komplex beschreiben
lassen. (Das mag sich paradox anhören, ist aber wirklich einfacher!). Dabei
entspricht der Amplitude samt ihrer Dämpfung der Imaginärteil der Frequenz
und der Phase einer Welle. Allerdings verwenden die Elektrotechniker statt des
„i“ der Mathematik das Symbol „j“, was aber unwesentlich ist.  Zahlensysteme Zahlensysteme
| Dual | Quartal | Oktal | Dezimal | Hexadezimal | | 0 | 0 | 0 | 0 | 0 | | L | 1 | 1 | 1 | 1 | | L0 | 2 | 2 | 2 | 2 | | LL | 3 | 3 | 3 | 3 | | L00 | 10 | 4 | 4 | 4 | | L0L | 11 | 5 | 5 | 5 | | LL0 | 12 | 6 | 6 | 6 | | LLL | 13 | 7 | 7 | 7 | | L000 | 20 | 10 | 8 | 8 | | L00L | 21 | 11 | 9 | 9 | | L0L0 | 22 | 12 | 10 | A | | L0LL | 23 | 13 | 11 | B | | LL00 | 30 | 14 | 12 | C | | LL0L | 31 | 15 | 13 | D | | LLL0 | 32 | 16 | 14 | E | | LLLL | 33 | 17 | 15 | F | | L0000 | 40 | 20 | 16 | 10 | | L000L | 41 | 21 | 17 | 11 | | : | : | : | : | : | | LLLLL | 73 | 37 | 31 | 1F | | L00000 | 80 | 40 | 32 | 20 | | L0000L | 81 | 41 | 33 | 21 | | : | : | : | : | : | | L00000000 | 640 | 320 | 256 | 100 | | L00000000000 | 10240 | 5120 | 4096 | 1000 | | : | : | : | : | : |
|







 Zahlensysteme
Zahlensysteme